В геометрии понятие "сумма ромба" может иметь несколько значений в зависимости от контекста. Рассмотрим основные математические характеристики ромба, которые могут подразумеваться под этим термином.
Содержание
В геометрии понятие "сумма ромба" может иметь несколько значений в зависимости от контекста. Рассмотрим основные математические характеристики ромба, которые могут подразумеваться под этим термином.
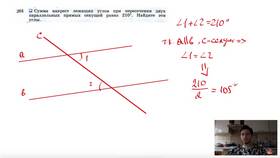
Сумма углов ромба
Как и любой четырехугольник, ромб обладает следующими свойствами суммы углов:
| Характеристика | Значение |
| Сумма внутренних углов | 360° |
| Каждый угол в правильном ромбе | 90° (квадрат - частный случай ромба) |
Свойства углов ромба
- Противоположные углы равны
- Сумма соседних углов составляет 180°
- Диагонали делят углы пополам
Сумма длин сторон ромба (периметр)
Поскольку все стороны ромба равны, периметр вычисляется по формуле:
P = 4 × a, где a - длина стороны ромба
Пример расчета
- При длине стороны 5 см: P = 4 × 5 = 20 см
- При длине стороны 12 м: P = 4 × 12 = 48 м
Другие возможные "суммы" ромба
В различных контекстах под "суммой ромба" могут подразумевать:
- Сумму длин диагоналей (d₁ + d₂)
- Сумму площадей треугольников, на которые делят ромб диагонали
- Результат сложения векторов, образующих стороны ромба
Математические свойства
| Параметр | Формула |
| Площадь | (d₁ × d₂)/2 |
| Высота | S/a |
Таким образом, понятие "сумма ромба" требует уточнения контекста - речь может идти о сумме углов, периметре или других характеристиках этой геометрической фигуры.
